27) 측지 방정식
추가로 설명된 바와 같이, 질량은 시공간을 휘게 만들고 다른 물체는 이 휘어진 시공간에서 측지선 곡선을 만듭니다.
하나이 때 굽힘 각도는 “측지선 방정식”으로 계산할 수 있습니다.
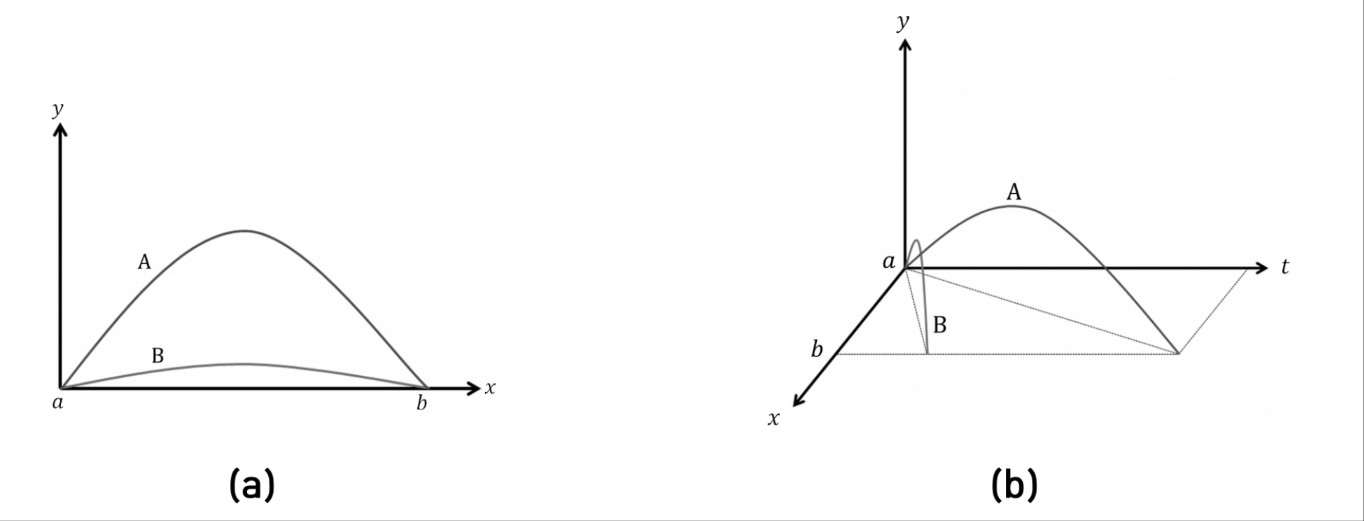
앞서 등가 원리를 설명할 때 중력은 가속 효과일 뿐이라고 했습니다.
그런 다음 위의 (a)와 같이 균일한 중력장 아래에서 $a$에서 $b$까지 두 개의 공 $A$와 $B$가 서로 다른 경사각으로 던져졌다고 가정합니다.
이때 두 구가 그리는 포물선은 서로 다른 궤도를 갖는다.
두 공 모두 동일한 중력장에 종속되므로 동일한 가속도를 갖습니다.
중력이 가속 효과일 뿐이라면 $A$와 $B$ 두 개의 총알이 같은 가속도로 같은 궤적을 따라가는 것이 당연하지 않을까요?
이에 대해 아인슈타인은 3차원 공간 궤적은 다르지만 4차원 시공 궤적은 같다고 주장한다.
위에서 언급한 중력장 방정식은 4차원 시공간과 관련된 방정식이므로 그림 (a)는 (b)와 같이 전개되어야 한다.
물체의 궤적, 즉 곡률을 공간뿐만 아니라 두 개의 시공간 정보로 계산하면 위 그림에서 $A$와 $B$ 두 공이 그리는 경로의 곡률은 같다.
. 아인슈타인에 따르면 같은 중력장이 만드는 4차원 시공간의 곡률은 같다.
이러한 4차원 시공간에서 측지선에 대한 정보를 제공하는 측지선 방정식은 다음과 같다.
$$\frac{d^2 x^{\lambda}}{dt^2} + \Gamma^{\lambda}_{\mu \nu } \frac{dx^{\mu }}{dt} \frac {dx^{\nu}}{dt} = 0$$ 여기서 $x$는 4D 표면의 좌표, $t$는 시간, $\Gamma^{\lambda }_{\mu \nu }$ ‘Christoffel Triad Symbol'(크리스토펠 기호)의미 측지선 방정식은 비선형 상미분 방정식의 시스템이며 중력장 방정식과 마찬가지로 풀기 매우 어려운 방정식입니다.
이 방정식의 왼쪽 첫 번째 항의 차원은 가속도를 나타내며 물체에 힘이 작용하지 않을 때 물체의 가속도 크기는 0입니다.
즉, 이때 객체는 측지선을 따라 일정한 속도로 움직이고 있습니다.
물체가 평면에 있을 때는 직선으로 움직이지만 곡면에 있을 때는 측지선을 따라 움직입니다.
1916년 아인슈타인은 완벽한 슈바르츠실트 해를 구하면서 얻은 크리스토펠 기호를 측지선 방정식과 중력장에서 빛이 휘는 각도에 대입하여 다음과 같이 표현했다.
$\delta$구조되었습니다.
$$\delta = \frac{4GM}{c^2 R}$$ 여기서 $G$는 중력 상수, $c$는 빛의 속도, $M$은 구형 물체의 질량, $R$은 구형 물체의 반지름입니다.
이 방정식을 사용하여 아인슈타인은 빛이 태양에 접근할 때 휘어지는 각도가 $\delta$임을 발견했습니다.
= 1.75”( = (1.75 / 3600)도).
아인슈타인의 이론적인 계산은 1919년 5월의 개기 일식을 기반으로 했습니다.
Eddington과 Cromelin은 각각 아프리카의 Principe Island와 브라질의 Sobral에서 관측을 통해 확인되었습니다.
2실제로 관측된 값은 Eddington이 $\delta$ = 1.98”, Cromelin $\delta$ = 0.93”이었다.
그 후 1919년 11월에 출판된
그 결과 물체와 시공간 간의 상호작용을 다루는 이론인 일반상대성이론이 과학계에 받아들여졌고, 1979년 개기일식 때 그리니치 천문대에서 빛의 회절을 새롭게 관측한 결과 에딩턴이 받은 데이터와 유사한 결과가 나왔다.
.
28) 중력 렌즈 효과
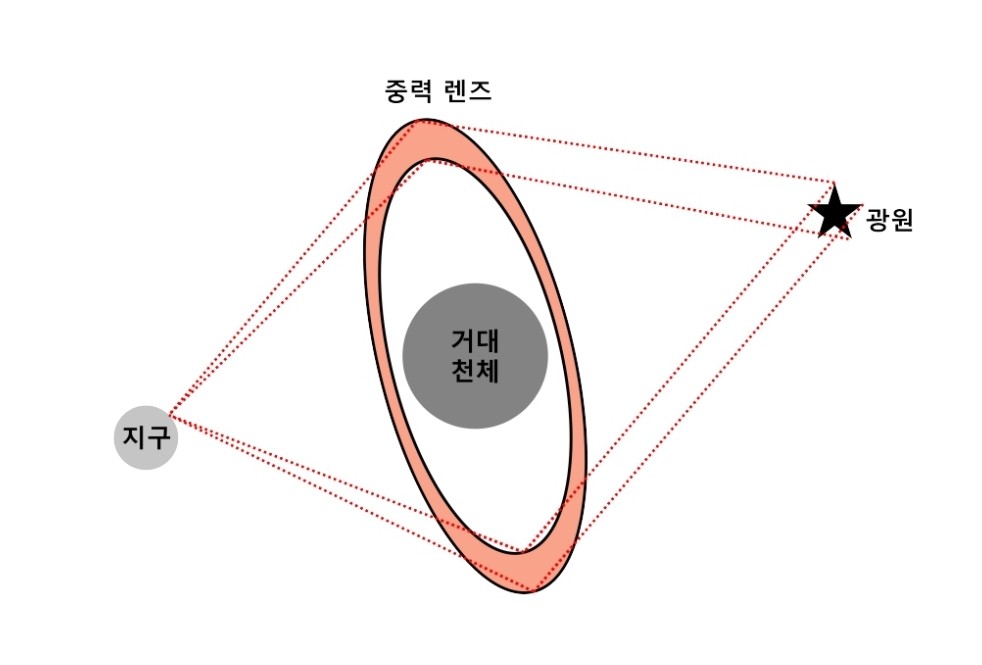
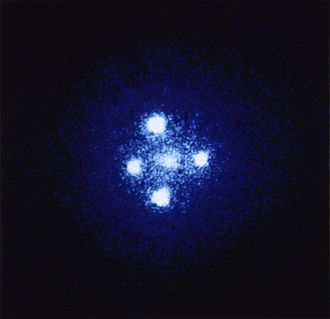
이러한 빛의 회절로 인해 발생하는 현상 중 하나가 “중력 렌즈 효과”입니다.
그림 3에서 보는 바와 같이 우주의 광원에서 나온 빛이 은하와 같은 큰 천체 주변의 중력장에 의해 휘어져 지구에 진입하면 원을 그리며 휘어지는 것처럼 보인다.
실제로 이런 원 안에 천체가 관측되는 현상은 흔한데, 완전한 고리로 나타날 때 ‘아인슈타인의 고리’라고 부른다.
어떤 경우에는 고리로 나타나지 않고 드물게 관찰되는데, 이 경우 대기 산란으로 인해 점으로 관찰된다.
29) 수성의 근일점
케플러가 발견한 행성의 운동 법칙에 따르면 태양계의 행성은 타원궤도를 그리며 태양 주위를 공전하므로 태양과 가장 가까운 지점인 ‘근일점’이 존재한다.
고전역학의 만유인력의 법칙에 따르면 태양과 행성 사이에 작용하는 중력은 거리의 제곱에 반비례하고 각 천체의 질량의 곱에 비례하기 때문에 근일점은 움직이지 않아야 한다.
그러나 실제로 행성의 근일점은 다른 행성과의 상호작용으로 인해 시간이 지남에 따라 이동하는 것으로 알려져 있으며, 수성의 경우 근일점은 100년에 약 5,600인치를 이동합니다.
그러나 그 중 지축의 세차운동에 의한 영향은 5,026인치, 다른 행성의 중력에 의한 영향은 531인치로 계산되어 나머지 43인치의 행방은 알 수 없다.
이 43”의 소재를 기존의 뉴턴 역학으로 설명할 수 없었기 때문에 많은 천문학자들은 수성과 태양 사이에 관측되지 않는 물체인 “화산”이 있다는 임시 가설을 발전시켰습니다.
삼선물들
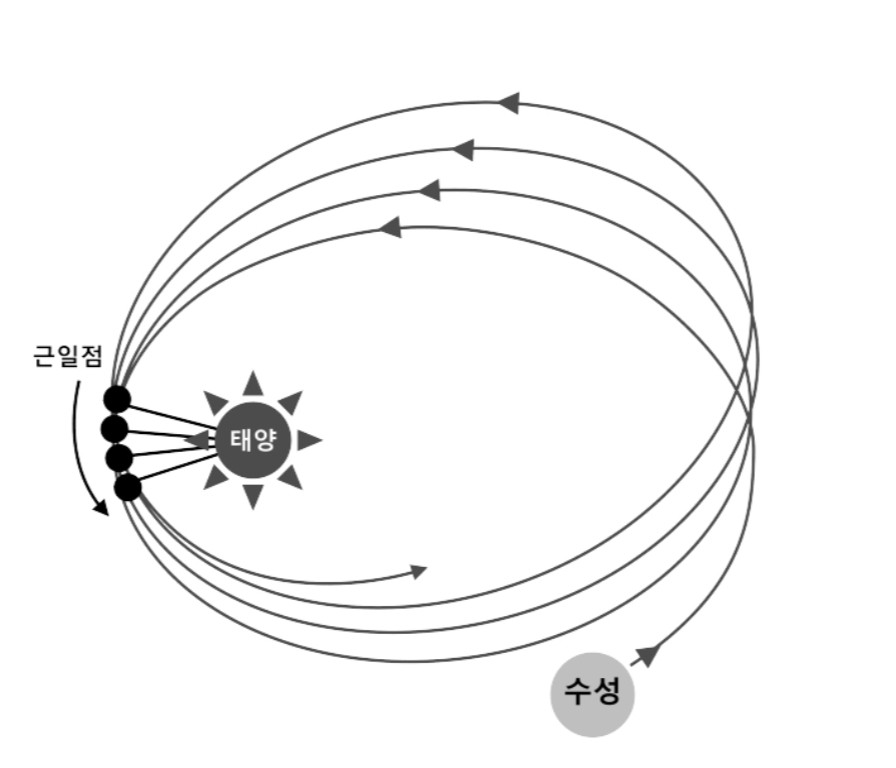
이 문제는 1915년 아인슈타인의 일반 상대성 이론에 관한 논문으로 해결되었습니다.
위의 그림에서 볼 수 있듯이 수성의 근일점은 태양이 수성 궤도의 시공간을 왜곡함에 따라 더 많은 각도로 움직입니다.
이를 측지선 방정식에서 구하면 각도는 $\delta$
$$\delta = \frac{6 \pi G^2 m^2 M^2}{c^2 L^2} \simeq 43.0”$$여기서 $m$은 수성의 질량, $M$은 태양의 질량, $L$은 수성의 근일점에서 각운동량의 크기, $G$는 중력 상수, $c$는 다음과 같이 계산됩니다.
빛의 속도. 측지선 방정식에 의해 계산된 값은 위에서 언급한 누락된 값 43”과 정확히 일치합니다.
이것은 미지의 행성인 Vulcan이 존재하지 않는다는 것을 보여주며, Mercury의 근일점 이동이 잘 설명됩니다.
하나공간에서 두 지점 사이의 최단 경로.
2강한 중력장, 즉 태양 근처에서 빛의 곡률을 관찰하기 위해서는 별의 빛이 햇빛에 의해 방해받지 않는 개기 일식이 가장 적합한 시간이었습니다.
삼주장을 정당화하기 위해 도입된 일종의 임시 가설.